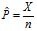Let the random variables X1, X2,……….,Xn denote a random sample from a population. The sample mean value of these random variables is defined as
Consider the sampling distribution of the random variable
 . At this point we cannot determine the shape of the sampling distribution, but we can determine the mean and variance of the sampling distribution. We know that the expectation of a linear combination of random variables is the linear combination of the expectations:
. At this point we cannot determine the shape of the sampling distribution, but we can determine the mean and variance of the sampling distribution. We know that the expectation of a linear combination of random variables is the linear combination of the expectations:Thus, the mean of the sampling distribution of the sample means is the population mean. If samples of n random and independent observations are repeatedly and independently drawn from a population, then as the number of samples becomes very large, the mean of the sample means approaches the true population mean.
The variance of the sample mean is denoted by
 , is given by
, is given by and the corresponding standard deviation, called the standard error of
and the corresponding standard deviation, called the standard error ofStandard Normal Distribution for the Sample Means
Whenever the sampling distribution of the sample means is a normal distribution, we can compute a standardized normal random variable, Z, that has mean 0 and variance 1:Example: Suppose that the annual percentage salary increases for the chief executive officers of all midsize corporations are normally distributed with mean 12.2% and standard deviation 3.6%. A random sample of nine observations is obtained from this population and the sample mean computed. What is the probability that the sample mean will be less than 10%?
Example: A spark plug manufacturer claims that the lives of its plugs are normally distributed with mean 36,000 miles and standard deviation 4,000 miles. A random sample of 16 plugs had an average life of 34,500 miles. If the manufacture’s claim is correct, what is the probability of finding a sample mean of 34,500 or less?