X is the sum of a set of n independent Bernoulli random variables, each with probability of success P. As a result,
 is the mean of a set of independent random variables. The central limit theorem can be used to argue that the probability distribution for
is the mean of a set of independent random variables. The central limit theorem can be used to argue that the probability distribution for  can be modeled as a normally distributed random variable.
can be modeled as a normally distributed random variable.The mean and variance of the sampling distribution of the sample proportion
 can be obtained from the mean and variance of the number of success, X. E(X) = nP Var(X) = nP(1 – P)
can be obtained from the mean and variance of the number of success, X. E(X) = nP Var(X) = nP(1 – P)And, thus,
We see that the mean of the distribution of
The variance of is the variance of the population distribution of the Bernoulli random variables divided by n,
 is the population proportion, P.
is the population proportion, P.The standard deviation of
 , which is the square root of the variance, is called its standard error.
, which is the square root of the variance, is called its standard error.Sampling Distribution of the Sample Proportion
Let be the sample proportion of successes in a random sample from a population with proportion of success P. Then
be the sample proportion of successes in a random sample from a population with proportion of success P. Then1. The sampling distribution of
 has mean P:
has mean P:E(
 ) = p
) = p2. The sampling distribution of p has standard deviation
3. If the sample size is large, the random variable
is approximately distributed as a standard normal. This approximation is good if
nP(1 – P) > 9
Example: A random sample of 250 homes was taken from a large population of older homes to estimate the proportion of homes with unsafe wiring. If, in fact, 30% of the homes have unsafe wiring, what is the probability that the sample proportion will be between 25% and 30% of homes with unsafe wiring?
Solution: For this problem we have
P = 0.30 n = 250
We can compute the standard deviation of the sample proportion,
 , as
, asThe required probability is
Thus, we see that the probability that the sample proportion is within the interval 0.25 to 0.35, given P = 0.30, is 0.9146. This interval is called a 91.46% acceptance interval.
Example: It has been estimated that 43% of business graduates believe that a course in business ethics is very important for imparting ethical values to students. Find the probability that more than one-half of a random sample of 80 business graduates have this belief.
The probability of having one-half of the sample believing in the value of business ethics courses is approximately 0.1.
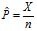







No comments:
Post a Comment